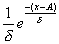Exponenciální rozdělení

Exponenciální rozdělení je vhodným modelem doby čekání na výskyt nějakého jevu, např. doby životnosti nějakého základního prostředku (tedy vlastně doby čekání na poruchu) apod. Toto rozdělení úzce souvisí s Poissonovým rozdělením. Jestliže totiž Poissonovo rozdělení modelovalo počet nějakých událostí v čase, exponenciální rozdělení se používá k modelování doby do výskytu příslušné události. Např. počet dopravních nehod na vybrané křižovatce za určitý časový interval se modeluje Poissonovým rozdělením, zatímco dobu od jedné nehody do druhé lze modelovat exponenciálním rozdělením.

Obě tato rozdělení sehrávají důležitou roli v teorii spolehlivosti. Časté aplikace jsou též v tzv. teorii hromadné obsluhy (teorie front), kde se pomocí exponenciálního rozdělení modeluje doba čekání ve frontě. To, že náhodná veličina X má exponenciální rozdělení s parametry A a d budeme zapisovat X ~ E(A,d). Hustota pravděpodobnosti tohoto rozdělení má tvar

Hustota pravděpodobnosti náhodné veličiny s exponenciálním rozdělením X ~ E(A,d)

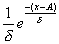 f(x) = ,     x  > A

 - Ą < A < Ą ,    d > 0

Parametr A se často interpretuje jako tzv. "parametr posunutí" rozdělení na ose x. Velmi často se při aplikacích setkáváme s "neposunutým" exponenciálním rozdělením, pro které A=0. Pak se tvar hustoty poněkud zjednoduší

f(x) = ,     x  > 0,  d > 0

Hustotu exponenciálního rozdělení pro Vámi zadané delta si můžete kreslit zde.
Distribuční funkce náhodné veličiny s exponenciálním rozdělením X ~ E(A,d)

F(x) = 1 - ,    x > A,  d > 0

 

Střední hodnota a rozptyl vypadají následovně:

Střední hodnota náhodné veličiny s exponenciálním rozdělením X ~ E(A,d)

E(X) = A + d

Rozptyl náhodné veličiny s exponenciálním rozdělením X ~ E(A,d)

 D(X) = d2

Pro ilustraci toho, jak zacházet s tímto rozdělením, uvádíme několik názorných příkladů. Budeme v nich předpokládat (pokud nebude výslovně uvedeno jinak), že parametr A = 0.

Vlastnosti exponenciálního rozdělení

Exponenciální rozdělení bývá někdy nazýváno "rozdělení bez paměti". Tento název je odvozen z této vlastnosti: Pravděpodobnost, že náhodná veličina X s rozdělením E(0,d) překročí hodnotu x+a podmíněná jevem X > a, je pro libovolné kladné a a x rovna nepodmíněné pravděpodobnosti jevu X > x, tj.

P[X > x+a/(X > a)] = P(X > x)

Pokud X značí dobu do poruchy nějakého zařízení, pak pravděpodobnost, že zařízení, které pracovalo bez poruchy po dobu a hodin, bude pracovat bez poruchy ještě alespoň x hodin, je rovna pravděpodobnosti, že zařízení, které dosud nebylo v provozu, bude pracovat alespoň x hodin, jako by "zapomnělo" dříve odpracovanou dobu. Tato vlastnost vysvětluje použití exponenciálního rozdělení v teorii spolehlivosti. Exponenciální rozdělení popisuje dobře rozdělení doby života zařízení, u kterých dochází k poruše ze zcela náhodných příčin a nikoliv v důsledku opotřebení (mechanické opotřebení, únava materiálu apod.). Má-li doba do výskytu události stejné exponenciální rozdělení, pak informace o tom, že událost nenastala po dobu a hodin, nemění pravděpodobnost výskytu události v příštích x hodinách.

Dalšími spojitými rozděleními jsou rozdělení odvozená z normálního rozdělení. Mezi ně patří tři další uvedená rozdělení.