Typy proměnných

Pro účely statistické analýzy je třeba u každé proměnné určit její typ. Některé současné programové statistické systémy ho umožňují zadávat při definování proměnné nebo jsou podle typů nabízeny statistické postupy.

V literatuře a programových systémech se můžeme setkat s různými způsoby klasifikace proměnných. V následujícím textu bude prezentován jeden z možných přístupů, který za hlavní kritérium považuje typy vztahů mezi hodnotami. Podle tohoto hlediska rozlišujeme proměnné nominální, ordinální, intervalové a poměrové.

Nominální proměnná je taková, o jejíž dvou hodnotách můžeme pouze říci, zda jsou stejné či různé (škola, fakulta, obor). Hodnotami mohou být texty (písmena), případně i číselné kódy. Lze u nich zjišťovat jen rozdělení četností, nemůžeme provádět aritmetické operace (sčítat apod.), výjimkou jsou binární proměnné (viz dále).

Ordinální (pořadová), u jejíž dvou hodnot můžeme navíc určit pořadí (úroveň spokojenosti, vzdělání). Jako hodnoty lze použít text, datum, číslo. Pro statistické analýzy (s výjimkou zjišťování četností) je třeba texty převést na čísla. S typem datum lze provádět jen některé výpočty, a to pouze v některých programových systémech.

Intervalová (rozdílová) proměnná je taková, pro jejíž dvě hodnoty můžeme navíc (k možnostem ordinální proměnné) vypočítat, o kolik je jedna hodnota větší (resp. menší) než druhá (měsíční příjem domácnosti, počet dětí v rodině). Hodnotami jsou tedy čísla.

Poměrová (podílová) proměnná je ta, pro jejíž dvě hodnoty můžeme navíc (k možnostem intervalové proměnné) vypočítat, kolikrát je jedna hodnota větší (resp. menší) než druhá, tzn. jedná se pouze o kladné hodnoty (počet členů domácnosti).

Nominální a ordinální proměnné jsou souhrnně označovány jako kvalitativní; intervalové a poměrové proměnné jsou souhrnně označovány jako kvantitativní (numerické), v české literatuře se můžeme setkat též s pojmem kardinální. Kvantitativní proměnné můžeme podle jiného hlediska dělit na

• diskrétní, které nabývají pouze celočíselných obměn (počet válců automobilu), a

• spojité (metrické), jež mohou nabývat libovolných hodnot z určitého intervalu (věk respondenta, cena výrobku, roční příjem domácnosti).

Nominální, ordinální a kvantitativní diskrétní proměnné můžeme souhrnně označit jako kategoriální (obměny těchto proměnných nazýváme kategoriemi). Podle jiného hlediska je můžeme dělit na

• dichotomické (alternativní), které nabývají pouze dvou kategorií (ekonomicky aktivní a neaktivní, kuřák a nekuřák), a

• vícekategoriální (množné), jež nabývají více než dvou kategorií (rodinný stav, obor).

U dichotomických proměnných se při výpočtech předpokládá, že jde o proměnné binární, které nabývají hodnot 0 a 1 (například číslo 1 znamená „ekonomicky aktivní“ a číslo 0 zase „ekonomicky neaktivní). Aritmetický průměr z těchto hodnot se rovná relativní četnosti hodnot 1 (tj. počet hodnot 1 vztažený k celkovému počtu pozorování):

Z důvodu výše uvedených vlastností se můžeme také setkat s členěním kategoriálních proměnných na dichotomické, nominální množné, ordinální a kvantitativní.

U dichotomických proměnných můžeme dále rozlišit proměnné

• symetrické, které mají obě kategorie stejné důležitosti (muž, žena) a

• asymetrické, jejichž jedna kategorie je důležitější (pacient se uzdravil).

Shrnutí

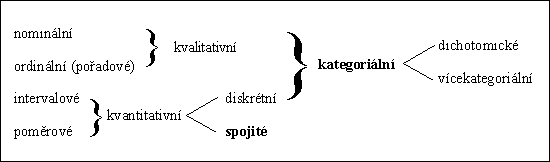
V datové matici se mohou vyskytovat proměnné nominální, ordinální, intervalové a poměrové, které lze ještě blíže specifikovat nebo zahrnout do širších skupin, viz schéma 1. Pro některé statistické metody používáme členění na proměnné kategoriální a kvantitativní spojité. Zvláštní místo zaujímají proměnné dichotomické.

Schéma 1 - Klasifikace proměnných

Poznámky

V literatuře se můžeme setkat též s definováním kategoriální proměnné v užším slova smyslu jako proměnné kvalitativní, případně pouze nominální (kvalitativní proměnná je někdy definována pouze jako nominální).

Proměnné určitého typu můžeme převádět na jiný typ, viz schéma 2.

Schéma 2 - Možnosti převodu typů proměnných

Upozornění

Hodnoty nominální množné proměnné mohou být označeny čísly, ale nelze s nimi provádět aritmetické operace. U ordinálních proměnných závisí možnost provádění aritmetických operací na předpokladu stejné vzdálenosti mezi kategoriemi.

Příklady

U každého příkladu vyberte z nabídky správný typ proměnné:

a)