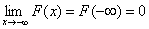Distribuční funkce

Definice: Distribuční funkce

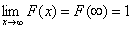
Distribuční funkci náhodné veličiny X budeme značit F(x) a definujeme ji následovně:

F(x) = P(X Ł x)                      pro všechna reálná x.

 

Distribuční funkce je tedy funkce, která každému reálnému číslu přiřazuje pravděpodobnost, že náhodná veličina nabude hodnoty, která je menší nebo rovna tomuto číslu.

Distribuční funkce má řadu vlastností, které vyplývají přímo z její definice.

1. distribuční funkce je nezáporné číslo menší nebo rovné jedné

0 Ł F(x) Ł 1

2. distribuční funkce je neklesající, tj. pro každé x1 Ł x2 platí F(x1) Ł F(x2)

3. distribuční funkce je spojitá zprava

4. 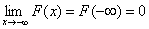a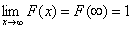

 a pokud obor možných hodnot M = { x; x Î (a,b) }, potom

 F(a) = 0 a F(b) = 1.

Dále je třeba si uvědomit, že platí následující: pravděpodobnost, že náhodná veličina nabude hodnoty z intervalu (x1,x2), je rovna rozdílu distribuční funkce v bodě x2 a x1, tj.

 P(x1 < X Ł x2) = F(x2) - F(x1)               pro  - Ą < x < Ą

Podle toho, jakých může náhodná veličina nabýt hodnot (resp. z jakého intervalu), rozlišujeme spojitou a diskrétní náhodnou veličinu, přesněji řečeno náhodnou veličinu se spojitým a diskrétním rozdělením.

O diskrétním rozdělení hovoříme tehdy, jestliže náhodná veličina nabývá pouze hodnot z nějaké konečné či spočetné množiny. Jedná se nejčastěji o celočíselné náhodné veličiny, např. počet zákazníků ve frontě (0,1,2,...), počet členů domácnosti (1,2,3,...), počet dopravních nehod za jeden den na území hlavního města Prahy (0,1,2,...), součet ok při hodu třemi kostkami (3,4,...,18) apod.

Poznámka: Distribuční funkci je možné definovat i pomocí ostré nerovnosti. Pak by její definice měla tvar: Distribuční funkce je funkce, která každému reálnému číslu přiřazuje pravděpodobnost, že náhodná veličina nabude hodnoty, která je menší než toto číslo.Vlastnost 3 by se pak změnila na spojitost zleva. Rozlišení těchto dvou definic má smysl jen tehdy, pokud distribuční funkce vykazuje body nespojitosti - tedy především u nespojité náhodné veličiny.