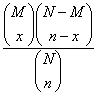pro x = max(0, M - N + n), ..., min(M, n)Mějme konečný soubor N jednotek (např. výrobků), z nichž M jednotek má sledovanou vlastnost A (např. výrobek je zmetek). Z tohoto souboru vybereme náhodně najednou nebo postupně (bez vracení) n jednotek. Nechť X značí počet vybraných jednotek majících sledovanou vlastnost A. Pak pravděpodobnosti P(X = x) pro tuto náhodnou veličinu jsou dány následujícím výrazem:
P(X = x) =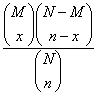
pro x = max(0, M - N + n), ..., min(M, n)
Přitom N, M a n jsou přirozená čísla, 1 Ł n < N, 1 Ł M < N.
Takováto náhodná veličina má potom hypergeometrické rozdělení s parametry N, M a n, což budeme zapisovat - X ~ Hg(N, M, n).
Pravděpodobnostní model pro toto rozdělení si můžeme představit i následovně: celkem máme k dispozici konečný soubor N jednotek, který je rozdělen na dvě skupiny. Jedna skupina má požadovanou vlastnost a má rozsah M jednotek, druhá skupina požadovanou vlastnost nemá a má rozsah N - M jednotek (součet rozsahů v první skupině a ve druhé skupině musí dát celkový počet N jednotek, což je splněno). Nyní náhodně vybereme n jednotek z celého konečného souboru o N jednotkách (přičemž samozřejmě nevíme, z které skupiny vybíráme) a zajímá nás pravděpodobnost, že x jednotek z n má požadovanou vlastnost - tedy že x jednotek bude pocházet z první skupiny, kde je M jednotek, a zbývajících n-x jednotek ve výběru tedy musí pocházet z druhé skupiny, která obsahuje N - M jednotek. Protože nám nezáleží na pořadí, v jakém jsou jednotky taženy, jedná se o kombinace (bez opakování). Po tomto vysvětlení se snad již vzorec pravděpodobnostní funkce hypergeometrického rozdělení jeví srozumitelnější.
Na rozdíl od předchozích rozdělení, při opakování tohoto náhodného pokusu je pravděpodobnost nastoupení sledovaného jevu závislá na výsledcích předcházejících pokusů, to znamená, že opakované náhodné pokusy jsou závislé.
Výpočty hodnot pravděpodobnostní funkce a výše uvedených charakteristik si můžete vyzkoušet zadáním vlastních hodnot: