Poloha je u nominální proměnné charakterizována modální kategorií, což je kategorie s největší četností. Jestliže jsou kategorie označeny indexem i (i = 1, 2, …, K, kde K je počet kategorií), ni jsou absolutní četnosti a pi relativní četnosti, pak max ni = nMo a max pi = pMo. Tyto četnosti modální kategorie se rovněž nazývají modální.
U sledované proměnné se může vyskytovat buď jedna nebo více modálních kategorií. V prvním případě jde o rozdělení četností unimodální, ve druhém případě o k-modální rozdělení, kde k je počet modálních kategorií. Konkrétně při výskytu dvou modálních kategorií se rozdělení nazývá bimodální a při třech těchto kategoriích jde o trimodální rozdělení.
Jestliže pMo> 0,5 , pak můžeme modální kategorii označit též jako majoritní a četnosti nMo a pMo rovněž jako majoritní.
![]() =
=
![]() .
.
Jako míry variability pak slouží
a) variační poměr v, který spočítáme podle vzorce v = 1 - nMo /n = 1 - pMo ,
b) nominální rozptyl nomvar (Ginniho odchylka), vyjadřující relativní počet všech dvojic, které nejsou ve stejné kategorii, a počítaný dle vzorce
nomvar =
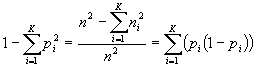 ,
,
c)
entropie H, která je
dána vzorcem
![]() .
.
Víme, že pMoÎ<1/K;1>
a rovněž
![]() Î<1/K;1>.
Tudíž vÎ<0;(K-1)/K>
a také nomvarÎ<0;(K-1)/K>.
Pro entropii platí, že HÎ<0;lnK>.
Jestliže míra variability nabude hodnoty nula, pak hovoříme o nulovém
rozptýlení, čili úplné homogenitě. Platí, že čím vyšší je hodnota,
která charakterizuje variabilitu, tím vyšší je heterogenita souboru.
Î<1/K;1>.
Tudíž vÎ<0;(K-1)/K>
a také nomvarÎ<0;(K-1)/K>.
Pro entropii platí, že HÎ<0;lnK>.
Jestliže míra variability nabude hodnoty nula, pak hovoříme o nulovém
rozptýlení, čili úplné homogenitě. Platí, že čím vyšší je hodnota,
která charakterizuje variabilitu, tím vyšší je heterogenita souboru.
Míry variability mohou být vyjadřovány také pomocí hodnot z intervalu od 0 do 1, čehož dosáhneme tím, že hodnotu vypočítanou podle některého z výše uvedených vzorců dělíme maximálně možnou hodnotou, tj. (K-1)/K, resp. lnK. Používány jsou míry
- normalizovaný nominální rozptyl norm. nomvar, pro který platí
norm. nomvar = K×nomvar/(K-1) , norm. nomvarÎ<0;1>,
- normalizovaná entropie H*, daná vztahem
H*=H/lnK , takže H*Î<0;1>.
Výpočty výše uvedených charakteristik si můžete vyzkoušet na základě absolutních četností ni (pouze přirozená čísla a nula) pro jednotlivé kategorie, které zadáte do následujících políček (nemusíte vyplnit všechna):