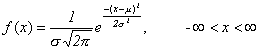
Jedním z nejdůležitějších spojitých rozdělení je normální rozdělení. Normální rozdělení má zcela zásadní význam v teorii pravděpodobnosti a matematické statistice a řídí se jím (alespoň "přibližně") mnoho náhodných veličin. Nejběžnějším typem takových veličin jsou náhodné chyby (chyby měření, způsobené velkým počtem neznámých a vzájemně nezávislých příčin). Proto se normálnímu rozdělení někdy říká rozdělení chyb. Rovněž mnohé náhodné veličiny v obchodě a ekonomii se řídí tímto rozdělením nebo jejich rozdělení jím může být velmi dobře aproximováno. Jako příklad uveďme třeba velikost zisku z cenných papírů, čas jež zabere vykonání určitého úkolu, hmotnost balíčku s moukou plněného automatem apod. Tímto rozdělením se dále řídí některé fyzikální a technické veličiny.
Někdy se rovněž můžeme setkat s označením Gaussova křivka pro označení hustoty normálního rozdělení, podle jednoho z praotců tohoto rozdělení.
Normální rozdělení je jednovrcholové rozdělení symetrické okolo střední hodnoty, kterou budeme značit µ. Střední hodnota tohoto rozdělení je rovna modu a mediánu. Hustota pravděpodobnosti má zvonovitý tvar - maxima dosahuje ve střední hodnotě. Náhodná veličina X, jež se tímto rozdělením řídí, může nabýt hodnoty od -Ą do +Ą. "Konce" tohoto rozdělení vypadají, jako by se již dotýkaly osy x, nikdy se jí však nedotknou, i když jsou jí tím blíže, čím více se vzdalujeme od střední hodnoty µ - ať již doleva či doprava. To, že se náhodná veličina řídí normálním rozdělením s parametry µ a s2, zapisujeme X ~ N(µ,s2).
Normální rozdělení má velmi příjemnou vlastnost a sice tu, že je jednoznačně určeno střední hodnotou a rozptylem, jež jsou jeho parametry. Pokud tedy tyto dvě charakteristiky známe, můžeme určit lehce již vše ostatní - to je tvar celého rozdělení.
Normální rozdělení je však velmi důležité i z dalších důvodů. Jeho význam spočívá především v tom, že za určitých podmínek dobře aproximuje řadu jiných (i diskrétních) pravděpodobnostních rozdělení.
Při řešení pravděpodobnostních úloh se často předpokládá, že sledovaná náhodná veličina má normální rozdělení, ačkoliv její skutečné rozdělení má jen podobný tvar, tzn. je jednovrcholové a přibližně symetrické. Tento postup je samozřejmě teoreticky podložen, jak dále uvidíme, a je velmi výhodný, neboť usnadňuje teoretické řešení mnoha problémů i praktické výpočty.
Hustota pravděpodobnosti zapsaná vzorcem vypadá takto:
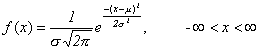
pro - Ą < µ < Ą , s2 > 0
A jak již bylo řečeno, základní charakteristiky mají tvar:
E(X) = µ
D(X) = s2
V programových systémech je třeba obvykle jako parametry normálního rozdělení zadat střední hodnotu a směrodatnou odchylku. Hustotu pravděpodobnosti náhodné veličiny X s normálním rozdělením si pro různé parametry můžete nechat nakreslit zde nebo na adresách http://www.stattucino.com/berrie/dsl/index.html a http://www-stat.stanford.edu/~naras/jsm/NormalDensity/NormalDensity.html.
Ilustrace aproximace binomického rozdělení normálním rozdělením se nachází na stránce http://www.ruf.rice.edu/~lane/stat_sim/normal_approx/index.html, aproximace Poissonova rozdělení na stránce http://www.stattucino.com/berrie/dsl/poissonclt.html. Aproximace některých charakteristik (průměrů, směrodatných odchylek) náhodných veličin se zadaným rozdělením je demonstrována na stránce http://www.ruf.rice.edu/~lane/stat_sim/sampling_dist/index.html.
Hodnoty distribuční funkce se dají určit pouze velmi těžce, neboť integrál
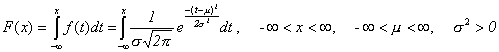
se řeší velmi náročným způsobem. Je tedy nesnadné určit obecně pravděpodobnost P(X Ł x) pro libovolné x. Z tohoto důvodu jsou hodnoty distribuční funkce tabelovány. Nelze samozřejmě tabelovat tyto hodnoty pro všechna možná µ a s2 a jejich kombinace. I to lze však elegantně vyřešit, jak vzápětí uvidíme.
Je důležité si připomenout, že plocha pod křivkou hustoty má velikost 1. Jinými slovy, integrál z hustoty přes celý definiční obor náhodné veličiny je roven jedné. Protože hustota je symetrická kolem střední hodnoty, znamená to, že střední hodnota dělí plochu pod křivkou na dvě stejné části - každá z nich má tedy velikost 1/2. Ze symetrie vyplývají samozřejmě i další příjemné vlastnosti. Předpokládejme, že chceme určit pravděpodobnost P(x1 < X < x2) náhodné veličiny X a přitom x1 a x2 jsou od střední hodnoty stejně vzdáleny. Tedy můžeme psát
| x1 - µ | = | x2 - µ |
Potom velikost plochy pod křivkou hustoty od x1 do µ je stejná, jako velikost plochy od µ do x2. A tedy
P(x1 < X < x2) = 2.P(x1 < X < µ) = 2.P(µ < X < x2)
Tato vlastnost vyplývající ze symetrie normálního rozdělení
nám velmi zjednoduší některé úvahy a výpočty.
Pro výpočty kvantilů náhodné veličiny X s normálním rozdělením existují různé programové prostředky, např. na adrese http://www-stat.stanford.edu/~naras/jsm/FindProbability.html (pouze pro N(0,1)) nebo na adrese http://psych.colorado.edu/~mcclella/java/normal/accurateNormal.html.
Velmi důležitým případem normálního rozdělení je rozdělení N(0,1). Tedy normální rozdělení s parametry µ = 0 a s2 = 1. Toto rozdělení se nazývá normované (standardizované) normální rozdělení. Má-li náhodná veličina U rozdělení N(0,1), pak její hustota pravděpodobnosti má tvar
f(u) = ![]() -Ą <
u < Ą
-Ą <
u < Ą
Distribuční funkci standardizovaného rozdělení budeme značit F. Tato funkce bude mít tvar:
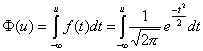
Tento tvar normálního rozdělení je symetrický kolem střední hodnoty µ = 0. Platí pro něj tedy
f(-u) = f(u) - Ą < u < + Ą
a opět ze symetrie dostáváme pro distribuční funkci
F(-u) = 1 - F(u) -Ą < u < + Ą .
Důležité je toto rozdělení zejména z toho důvodu, že jeho hodnoty jsou tabelovány. To by samozřejmě samo o sobě nic neznamenalo, pokud by neexistoval způsob, jak normální rozdělení s libovolnými parametry transformovat do této podoby. Tento způsob však existuje a nazývá se standardizace.
Srovnáme-li totiž dvě náhodné veličiny X ~ N(µ,s2) a U ~ N(0,1), pak lze dojít k následujícímu závěru. Velikost plochy pod křivkou hustoty "vlevo" a "vpravo" od jakéhokoliv bodu x, koresponduje s velikostí plochy "vlevo" a "vpravo" od příslušného bodu u, pokud jako míru vzdálenosti bereme směrodatnou odchylku s toho kterého rozdělení. Tedy velikost plochy u standardizované veličiny U mezi body 0 a 1 je stejná jako velikost plochy u normální náhodné veličiny X mezi body µ a µ + s. Podobně velikost plochy u standardizované veličiny U mezi body 0 a 2 (dvojnásobek směrodatné odchylky) je stejná jako velikost plochy u normální náhodné veličiny X mezi body µ a µ + 2s atd.
Pro ilustraci předpokládejme, že náhodná veličina X má normální rozdělení se střední hodnotou 500 a rozptylem 2500, tedy X ~ N(500,2500). Směrodatná odchylka je tedy rovna s = 50. Bude nás zajímat pravděpodobnost, že náhodná veličina X nabude hodnoty z intervalu (500,575), což symbolicky zapsáno je P(500 Ł X Ł 575). Pokud uplatníme výše uvedenou úvahu, dostáváme: střední hodnota veličiny X je 500 a odpovídá střední hodnotě 0 veličiny U. Hodnota 575 je vzdálena 1,5 násobku směrodatné odchylky (ta je rovna 50) od střední hodnoty 500 veličiny X, což odpovídá vzdálenosti 1,5 násobku směrodatné odchylky (ta je rovna 1) od střední hodnoty 0 veličiny U. Pak můžeme psát
P(500 Ł X Ł 575) = P(0 Ł U Ł 1,5)
a tedy
P(0 Ł U Ł 1,5) = F(1,5) - F(0)
Víme, že F(0) = 1/2 a tabulkách zjistíme, že F(1,5) = 0,93319. Tedy hledaná pravděpodobnost je rovna
P(500 Ł X Ł 575) = 0,93319 - 0.5 = 0,43319
Velmi lehce se můžeme přesvědčit o tom, že má-li náhodná veličina X rozdělení N(µ, s2), pak náhodná veličina
![]()
má rozdělení N(0,1).
Platí totiž
![]()
a
![]()
Můžeme tedy psát
U ~ N(0,1).
Naopak, pokud má náhodná veličina U normované normální rozdělení, tedy U ~ N(0,1) - potom náhodná veličina
X = µ + sU
má normální rozdělení s parametry µ a s2 - tedy můžeme psát
X ~ N(µ, s2).
Toto nám v podstatě dává návod, jak obecně postupovat při hledání pravděpodobnosti P(X Ł x) pro normální rozdělení s jakýmikoliv parametry µ a s2. Platí:
P(X Ł x) = ![]()
přičemž poslední pravděpodobnost v této rovnici se dá zjistit z tabulek (jedná se vlastně o hodnotu distribuční funkce normovaného normálního rozdělení v bodě (x-µ)/s ).
Že tato úprava je korektní, se můžeme lehce přesvědčit. Jestliže
X Ł x
potom
X - µ Ł x - µ
a
(X - µ)/s Ł (x - µ)/s (neboť s > 0).
Ze stejných důvodů platí pro pravděpodobnost P(x1 Ł X Ł x2) rovnost
P(x1 Ł
X Ł
x2) = ![]()