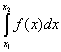Věnujme se nyní formě popisu spojité náhodné veličiny. Jestliže náhodná veličina může nabýt jakékoliv hodnoty z určitého intervalu, hovoříme o náhodné veličině se spojitým rozdělením. Jako příklad lze uvést: životnost pračky (0, Ą), výška člověka (0, Ą), délka určitého předmětu (0, Ą), náhodně vybrané reálné číslo (-Ą, Ą) apod. V takovém případě je možné použít k popisu rozdělení náhodné veličiny rovněž hustotu pravděpodobnosti.
Hustota pravděpodobnosti f(x) spojité náhodné veličiny X je nezáporná reálná funkce taková, že pro všechna reálná x se dá distribuční funkce F(x) náhodné veličiny X vyjádřit ve tvaru
![]()
pro - Ą < x < Ą
Obsah plochy mezi touto křivkou f(x) a osou x v jakémkoliv intervalu je pravděpodobnost,
že X nabude hodnoty z tohoto intervalu.To ostatně plně odpovídá tomu, jak jsme hustotu definovali - připomeňme,
že integrál z křivky je vlastně velikost plochy pod touto křivkou.
Vlastností každé hustoty pravděpodobnosti je, že celá plocha pod křivkou dává dohromady jedničku. To je analogické situaci u diskrétní náhodné veličiny, kde součet pravděpodobností všech možných výsledků rovněž dával jedničku. Pokud tuto vlastnost zapíšeme matematicky, dostáváme rovnici:
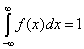
Jestli je f(x) = 0 pro všechna x Ł A a všechna x > B, pak je
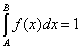
Dá se dále velmi lehce dokázat, že
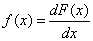
ve všech bodech, kde existuje derivace distribuční funkce. Známe-li tedy distribuční funkci, můžeme lehce určit hustotu pravděpodobnosti a naopak, známe-li hustotu pravděpodobnosti, snadno většinou spočítáme distribuční funkci.
Z vlastností distribuční funkce vyplývá, že pro spojitou náhodnou veličinu platí (pro nespojitou to pochopitelně platit nemusí):
P(X = x) = 0
pro každé reálné x. Tedy pravděpodobnost, že spojitá náhodná veličina nabude jedné zcela konkrétní hodnoty, je nulová. Potom tedy pro všechna reálná x1 < x2 je
P(x1 < X Ł x2)
= P(x1 Ł X < x2)
= P(x1 Ł X Ł
x2) = P(x1 < X <
x2) =