Chí-kvadrát test dobré shody

Nejznámějším a zřejmě nejpoužívanějším je test dobré shody. Testujeme hypotézu H₀: p_i = p_i,0 , kde i = 1,2,...,K (K je počet kategorií) a , vůči alternativní hypotéze H₁: H₀ neplatí. Jestliže se konstanty p_i,0 rovnají, pak můžeme nulovou hypotézu vyjádřit jako H₀: p₁ = p₂ = ... = p_K.

Pro np_i,0 ł 5 se používá testové kritérium chí-kvadrát: 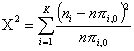. Tato náhodná veličina má za předpokladu, že platí hypotéza H₀, chí-kvadrát rozdělení s (K-1) stupni volnosti, tj. C² ~ C²(K-1). Vypočtenou hodnotu uvedeného testového kritéria C² proto porovnáváme s kvantilem C²_1-a. Jestliže zamítáme H₀, pak můžeme vytvořit znaménkové schéma odchylek, přičemž pro n ł 30 np_i,0 > 5 využijeme aproximaci normovaným normálním rozdělením. Pro každou kategorii i vypočítáme normovanou hodnotu . 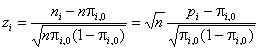Tyto hodnoty pak porovnáváme s kvantily náhodné veličiny s normovaným normálním rozdělením a určujeme stupeň odchýlení od hodnot p_i,0.

Výstupem z programových systémů jsou empirické a teoretické četnosti pro jednotlivé kategorie a též rozdíly těchto četností. K vlastnímu vyhodnocení testu se vztahuje tabulka s hodnotou testového kritéria, počtem stupňů volnosti a minimální hladinou významnosti, od které zamítáme hypotézu H₀.

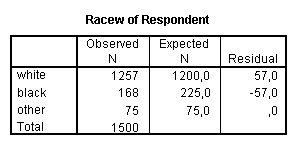
Výsledky chí-kvadrát testu pro různá zadání lze porovnávat na stránce http://www.ruf.rice.edu/~lane/stat_sim/chisq_theor/index.html.

Pro hrací zařízení, které by mělo se stejnými pravděpodobnostmi generovat čísla od 1 do n (dále bude nazýváno n stěnná "kostka") lze výsledky zjistit pomocí následující aplikace (n <= 100).