
V této kapitole budeme zkoumat statistické závislosti v datech. Velmi často se zkoumá závislost pro dvě proměnné. Používané metody jsou zaměřeny buď na vzájemnou závislost (souvislost) nebo na jednostrannou závislost. Kromě testů o nezávislosti dvou proměnných se zmíníme o testech zkoumajících, zda jsou dvě posloupnosti hodnot ze stejného rozdělení.
I v případě dvou proměnných bývá prvním krokem zobrazení rozdělení četností, a to buď v tabulce, nebo v grafu. U kategoriálních proměnných jsou četnosti zjišťovány pro všechny takové dvojice kategorií, kdy jedna kategorie z dvojice přísluší první proměnné a druhá kategorie druhé proměnné. Dostáváme tak dvourozměrnou tabulku četností, z jejichž hodnot již často můžeme usoudit na závislost či nezávislost mezi dvěma kategoriálními proměnnými, a nazývá se proto kontingenční tabulka. V políčkách jsou uváděny buď absolutní nebo relativní četnosti, které mohou být počítány třemi různými způsoby: řádková procenta (dostáváme 100 % v jednotlivých řádcích), sloupcová procenta (100 % ve sloupcích) a procenta vypočítaná na základě rozsahu souboru (100 % v celé tabulce). Můžeme buď zobrazit několik tabulek s různými typy četností, nebo zapsat několik hodnot do jednoho políčka (lze v SPSS). Kontingenční tabulka je základem pro testování závislostí a pro výpočet měr intenzity závislostí.
V programových systémech můžeme dvourozměrnou tabulku četností získat v různých grafických úpravách. Kontingenční tabulka může být zobrazena například v následujícím tvaru:

Ve výše uvedeném příkladu bychom mohli sledovat, zda se rozdělení proměnné zachycující míru štěstí liší v závislosti na pohlaví. Názornější proto bude, jestliže si necháme zobrazit řádková procenta.

Graficky lze hodnoty z tabulky zobrazit jako sloupkový graf, přičemž četnosti pro dvojice kategorií mohou být vyjádřeny jako shluk sloupků (graf shlukový) nebo jako části jednoho sloupku (graf kumulativní). Výšky nebo části sloupků mohou představovat kterýkoli z výše uvedených typů četností.
|
|
|
U dvou proměnných nás obvykle zajímá, zda mezi nimi existuje závislost. Tato závislost může být buď vzájemná nebo jednostranná. Sledujeme například vzájemnou závislost vztahu ženy k manželovi a vztahu ženy k dětem, ale jednostrannou závislost vztahu k dětem na vzdělání respondenta (opačná závislost nemá logicky smysl).
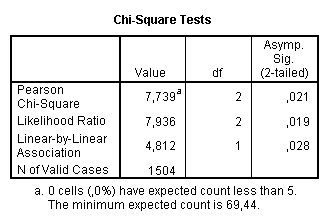
Základním testem je chí-kvadrát test o vzájemné nezávislosti v kontingenční tabulce. Jde o obdobu chí-kvadrát testu dobré shody, neboť testujeme shodu zjištěných a teoretických četností (přesněji řečeno, zda náš výběr je z takového základního souboru, kde jsou určité teoretické četnosti). Nesmíme zapomenout na předpoklad, aby teoretické četnosti v jednotlivých políčkách neklesly pod hodnotu 5 alespoň v 80 % políček a ve zbylých políčkách neklesly pod hodnotu 2.
Výsledek testu můžeme získat v následující podobě (SPSS). Protože v posledním sloupci se hodnoty nacházejí v intervalu od 0,01 do 0,05, lze konstatovat, že na 5% hladině významnosti zamítáme hypotézu o nezávislosti, zatímco na 1% hladině významnosti tuto hypotézu nezamítáme.
Pro ordinální proměnné můžeme použít test na nulovost Spearmanova koeficientu pořadové korelace (tj. test o vzájemné nezávislosti dvou proměnných). Výsledek testu můžeme získat v následujícím tvaru (SPSS). Protože v části "Sig." se vyskytuje téměř nulová hodnota, pak na jakékoli zvolené hladině významnosti zamítáme hypotézu o nezávislosti.

Chí-kvadrát test o nezávislosti a test na nulovost
Spearmanova koeficientu pořadové korelace patří k neparametrickým testům,
které nepředpokládají, že výběr je z nějakého určitého rozdělení
s určitými parametry (resp. že jde o velký výběr z nějakého
rozdělení s určitými charakteristikami).
Kromě těchto dvou nejznámějších testů určených ke zjištění vzájemné závislosti můžeme použít i testy na nulovost celé řady dalších měr intenzity závislosti, o nichž bude pojednáno dále.
Jako další typy neparametrických testů lze uvést ty, u nichž se zjišťuje shoda rozdělení pro dva výběry. Rozlišujeme testy pro dva nezávislé výběry a testy pro dva závislé výběry.
V prvním případě obvykle rozdělíme hodnoty jedné proměnné (Y) do dvou skupin, a to na základě dvou hodnot druhé proměnné (X). Tímto způsobem zjišťujeme, zda se pro různé hodnoty proměnné X liší podmíněná rozdělení četností proměnné Y, to znamená, zda proměnná X statisticky působí na proměnnou Y (jednostranná závislost).
Při dvou závislých výběrech obvykle sledujeme dvě proměnné, které obsahují údaje zjištěné v různých obdobích (plánovaný a skutečný počet dětí apod.), nebo které obsahují stejné kategorie (stupeň obliby dvou různých hudebních žánrů).
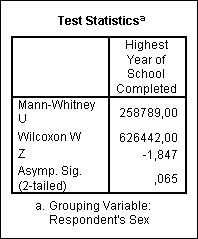
V SPSS je použit Mann-Whitneyův test, který je rozšířením Wilcoxonova testu. Wilcoxonova statistika (W) je získána tak, že je každé hodnotě přiřazeno pořadí v rámci všech hodnot (oba výběry jsou spojeny do jednoho celku) a je proveden součet těchto pořadí pro výběr menšího rozsahu. Mann-Whitneyova statistika (U) je počet výskytů případů, kdy ve výběru menšího rozsahu je určitá hodnota menší než hodnoty ve výběru většího rozsahu.
Výstupem jsou dvě tabulky. V první jsou údaje o pořadí pro oba výběry (počet pozorování, průměrné pořadí a součet pořadí), ve druhé výsledky testu, jejichž součástí je Mann-Whitneyova statistika U, Wilcoxonova statistika W a minimální hladina významnosti, od níž zamítáme hypotézu H0.

V SPSS jsou k dispozici tři typy testů: znaménkový, Wilcoxonův a McNemarův test.
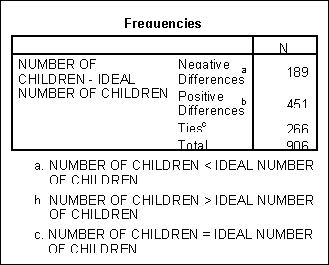
Test je založen na diferencích párových hodnot. Testujeme nulovou hypotézu, že medián diferencí je roven nule, vůči oboustranné alternativní hypotéze. Základem je počet znamének diferencí určitého typu (kladných nebo záporných), který je menší.
 |
 |
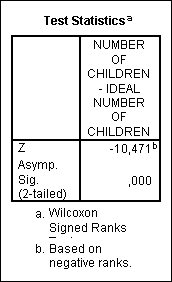
V tomto případě opět testujeme nulovou hypotézu, že medián diferencí je roven nule, vůči oboustranné alternativní hypotéze. Postupuje se tak, že nenulovým diferencím jsou přiřazena pořadová čísla. Zvlášť pro kladné a zvlášť pro záporné diference je pak vypočítán součet těchto pořadí. Základem testu je menší součet.

Lze použít pouze pro dvě dichotomické proměnné se stejnými kódy. Testuje se nulová hypotéza o shodě četností v políčkách mimo hlavní diagonálu (tj. v políčkách na vedlejší diagonále). Testové kritérium má za předpokladu platnosti nulové hypotézy chí-kvadrát rozdělení s jedním stupněm volnosti.


Jestliže proměnná X, která rozděluje hodnoty proměnné Y do skupin, nabývá více než dvou hodnot, můžeme získat více než dva nezávislé výběry. Pro porovnání rozdělení pak použijeme Kruskal-Wallisův test.
Výpočet testového kritéria je obdobně jako u testu pro dva výběry založen na pořadových číslech, která jsou přiřazena hodnotám v souboru, vzniklým spojením všech výběrů.
 |
 |