Dílčí korelační koeficienty

Pokud pracujeme s několika veličinami najednou, potřebujeme určit „čistou“ závislost mezi dvěma veličinami bez vlivu veličin ostatních. Pokud by šlo připravit pokus tak, aby při něm zůstaly eliminované proměnné neměnné, umožnilo by nám to ohodnotit závislost dvou sledovaných proměnných bez vlivu ostatních. To je však v praxi velmi náročné, ba téměř nemožné. Tato obtížnost vede k tomu, že se snažíme při výpočtu vyloučit vliv některých proměnných uměle, což nám umožňují právě dílčí korelační koeficienty. Dílčí korelační koeficient ve tvaru

se interpretuje jako jednoduchý korelační koeficient mezi Y a X při vyloučení vlivu Z,…,Q. Tento koeficient můžeme spočítat jako jednoduchý korelační koeficient náhodných složek ε¹ a ε² v regresních rovnicích

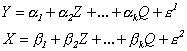
Pokud jsou veličiny, figurující v předchozích rovnicích, jen slabě lineárně závislé, nejsou velké rozdíly mezi jednoduchými a dílčími korelačními koeficienty. Naopak, existuje-li mezi těmito veličinami silná lineární závislost, jsou velké rozdíly i mezi hodnotami jednoduchých a dílčích korelačních koeficientů.

Dílčí korelační koeficienty se někdy označují jako parciální. Tyto koeficienty je možné počítat různými způsoby. Jednou z možností je i výpočet z korelační matice vektoru náhodných veličin (Y,X,Z,…,Q)´ , která má tvar

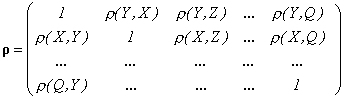
Z této matice pak určíme dílčí korelační koeficient jako

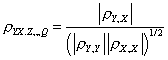
kde

je determinant matice ρ zmenšený o první řádek Y a druhý sloupec X atd.

Dílčí korelační koeficient můžeme počítat pro všechny možné podmnožiny veličin (X,Z,T,…,Q). Pak lze např. počítat

Další možností jak tento koeficient spočítat, je i rekurentní výpočet, kdy korelační koeficient vyššího řádu počítáme z korelačních koeficientů řádu nižšího. Navíc výpočet dílčích korelačních koeficientů bývá standardně výbavou běžných statistických programů.