Autokorelace reziduí

Podle jednoho z předpokladů pro náhodnou složku by tato měla mít charakter nekorelovaných náhodných veličin. Tuto vlastnost můžeme ověřit na základě analýzy reziduí. V tuto chvíli tedy na rezidua pohlížíme jako na konkrétní hodnoty náhodné složky z regresního modelu a celý test postavíme právě na hodnotách reziduí e_i.

Podívejme se ještě, jak vypadá autokorelační struktura prvního řádu:

ve které ρ je neznámý parametr. Analogicky bychom sestrojili autokorelační strukturu druhého, třetího řádu atd. Autokorelace prvního řádu se však vyskytuje nejčastěji.

K testu se používá Durbin-Watsonova statistika (slouží následně ke konstrukci odhadu parametru ρ) ve tvaru

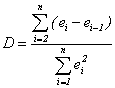
Hodnoty této statistiky se pohybují od nuly do čtyř. Pokud je tato statistika rovna číslu 2, rezidua nevykazují žádnou autokorelaci, hodnoty D menší než 2 značí pozitivní autokorelaci a hodnoty větší než 2 značí autokorelaci negativní. V praxi můžeme zjednodušeně postupovat takto: leží-li hodnota testové statistiky D v intervalu (1,4;2,6), rezidua nevykazují autokorelaci, hodnota pod 1,4 značí kladnou autokorelaci, hodnota nad 2,6 značí zápornou autokorelaci. To je však značně zjednodušený a vlastně i nekorektní přístup, protože správně by se měly hodnoty testové statistiky D srovnávat s příslušnými kritickými hodnotami či s příslušnými kvantily. Je tedy třeba uvedené pravidlo chápat jen jako orientační vodítko.