Vyrovnávací kritéria

 

Vyrovnávací kritéria jsou kritéria, pomocí kterých volíme nejvhodnější způsob odhadu parametrů regresní funkce. V této souvislosti se nám objevují nové pojmy:

napozorovaná (empirická) hodnota - hodnota proměnné, kterou jsme získali jako výsledek pozorování (měření, vážení atd.). V případě vysvětlované proměnné ji značíme Y.

odhadnutá (teoretická) hodnota - hodnota proměnné, kterou jsme získali jako výsledek modelování této proměnné. V případě vysvětlované proměnné ji značíme .

reziduum - rozdíl mezi napozorovanou a odhadnutou hodnotou. Reziduum značíme symbolem e a v příslušném bodě počítáme jako  . Reziduum tedy můžeme chápat jako velikost chyby, které se v příslušném bodě při odhadu dopouštíme.

 

Nejvhodnějším vyrovnávacím kritériem tedy bude takový postup odhadu parametrů regresní funkce, který dává nejmenší hodnoty reziduí (tedy „nejmenší chybu“) a to najednou ve všech odhadovaných bodech. Otázka je však složitější, neboť nestačí pouze rezidua sečíst - vlivem kladných a záporných znamének u jednotlivých hodnot by mohlo dojít k tomu, že součet reziduí bude nulový, přestože jednotlivá rezidua (tedy jednotlivé chyby) jsou veliké. Velkou roli při výběru metod odhadu sehrává též přítomnost odlehlých pozorování, která silně podmiňuje použitou metodu odhadu. Z celé škály vyrovnávacích kritérií se jako nejpoužívanější (ne však vždy nejhodnější) jeví metoda  nejmenších čtverců, na kterou se v našem popisu omezíme.

 

 

Metoda nejmenších čtverců

 

Metoda nejmenších čtverců je metoda pro odhad parametrů regresní funkce a to pouze pro takové modely, které jsou lineární v parametrech. Nelze ji tedy použít v případě nelineární regrese. Celá metoda je založena na minimalizaci reziduálního součtu čtverců, kde pod pojmem reziduální součet čtverců rozumíme výraz

Za odhadnutou hodnotu Y dosadíme do reziduálního součtu čtverců konkrétní tvar regresní křivky, poté výraz parciálně zderivujeme podle jednotlivých parametrů (hledáme minimum) a položíme roven nule. Tím obdržíme soustavu rovnic, jejichž řešením získáme konkrétní hodnoty parametrů. Celá metoda se nazývá metoda nejmenších čtverců (MNČ) a obdržená soustava rovnic se označuje jako normální soustava rovnic. O tom, že obdržíme skutečně minimum a nikoliv maximum, se můžeme přesvědčit na základě záporných hodnot druhých derivací uvedených rovnic. Celý postup budeme ilustrovat na příkladu, kdy regresní křivkou bude přímka. V případě jiných regresních funkcí se postupuje analogicky.

 

 

Metoda nejmenších čtverců pro přímku

 

Hledáme minimum  výrazu

kde

a

přičemž

 a  jsou konkrétní odhady příslušných parametrů. Po dosazení obdržíme

Zderivujeme výraz parciálně podle b₀  a b₁ a dostaneme soustavu normálních rovnic

 

 

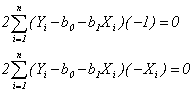
což po příslušných úpravách můžeme přepsat do tvaru

 

 

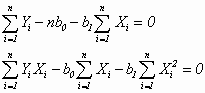
Z uvedených rovnic je zřejmé, že druhá derivace podle příslušných parametrů je záporná a jedná se tedy skutečně o minimum daného výrazu.