Dílčí t-testy

Dílčí t-testy jsou testy o hodnotách jednotlivých parametrů regresní funkce a umožňují nám testovat oprávněnost setrvání vysvětlující proměnné v regresním modelu. Testujeme (postupně pro jednotlivá i) nulovou hypotézu ve tvaru

H₀: β_i=0 pro i=0,1,…,k

proti alternativě

H₀: β_i ≠ 0 pro i=0,1,…,k

Pokud se ukáže, že pro konkrétní i nelze zamítnout nulovou hypotézu, je třeba zvážit setrvání příslušné vysvětlující proměnné v modelu. Pokud by se totiž parametr u příslušné proměnné neodlišoval významně od nuly, pak taková proměnná do modelu nic nového nepřináší a je v něm tudíž zbytečně. „Nadbytečnost“ proměnné v modelu by se však měla prokázat i podle jiných kritérií. Dále je však třeba poznamenat, že z hlediska kvality výsledných odhadů prováděných na základě regresního modelu je horší variantou případ, kdy proměnnou, která do modelu patří, chybně vyřadíme (testování hypotéz - chyba II. druhu) než případ, kdy proměnná do modelu nepatří a my ji tam chybně ponecháme (chyba I. druhu). Přitom je třeba si uvědomit, že pod kontrolou máme pouze pravděpodobnost chyby I. druhu, nikoliv však již pravděpodobnost chyby II. druhu.

Závěrem je třeba poznamenat, že vyřazení (či nové zařazení) proměnné do modelu znamená spustit celý proces tvorby modelu od začátku a tedy znamená to i nový odhad regresních parametrů.

Testová statistika pro tento test má Studentovo t-rozdělení s n-p stupni volnosti, kde p=k+1 a má tvar

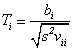
kde s² je nestranným odhadem rozptylu náhodné složky a v_ii jsou prvky matice

. Klasický postup by tedy vypadal tak, že spočítáme testovou statistiku, porovnáme její hodnotu s příslušnými kvantily a na základě tohoto srovnání vyslovíme závěr. Současná výpočetní technika a především statistické pakety nám však umožňují jednodušší postup, který bude patrný z následujícího výstupu z paketu Statgraphics.

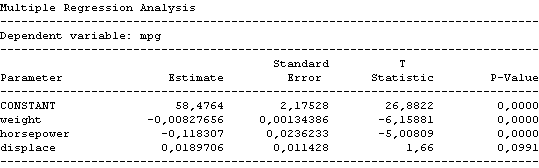
Poslední sloupec výstupu obsahuje hodnotu nadepsanou P-value. Tato hodnota představuje maximální možnou hladinu testu alfa, pro kterou hypotézu H₀ ještě nezamítneme. Pokud tedy hladina testu alfa bude větší než uvedená hodnota P-value, zamítneme H₀. Nebo obráceně, bude-li hodnota P-value menší než námi předem zvolená hladina testu, nulovou hypotézu zamítáme, v opačném případě nulovou hypotézu nelze zamítnout. Hodnota testové statistiky je uvedena v předposledním sloupci (T Statistics), ale využití P-value ji v podstatě ani nepotřebujeme. Stejným způsobem se za pomoci hodnoty P-value vyhodnocují i další testy ve všech statistických paketech (samozřejmě i mimo oblast regresní analýzy).