Chí-kvadrát rozdělení

Důležitým spojitým rozdělením, které má široké uplatnění, je chí-kvadrát rozdělení. Toto rozdělení je odvozeno ze součtu nezávislých náhodných veličin s normovaným normálním rozdělením. Formulujme nyní tuto informaci přesněji.

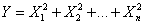
Pokud X1,X2,...,Xn jsou nezávislé náhodné veličiny, z nichž každá má rozdělení N(0,1), pak náhodná veličina

má rozdělení c2 (chí-kvadrát) o n stupních volnosti (které budeme stručně značit c2(n)).

Jediným parametrem tohoto rozdělení je počet stupňů volnosti n a je zřejmé, že toto rozdělení je definováno pouze pro y > 0.

Vzorec hustoty tohoto rozdělení má poměrně složitý tvar a nebudeme jej proto uvádět. Základní charakteristiky mají hodnotu:

Střední hodnota náhodné veličiny s c2 rozdělením o n stupních volnosti X ~ c2(n)

E(X) = n

Rozptyl náhodné veličiny s c2 rozdělením o n stupních volnosti X ~ c2(n)

D(X) = 2n

Pro zvyšující se počet stupňů volnosti se hustota tohoto rozdělení stále více blíží tvaru hustoty normálního rozdělení.

Kvantily tohoto rozdělení budeme značit obvyklým způsobem - 100a-procentní kvantil označíme Pa2(n). Hodnoty kvantilů lze najít v tabulkách.

Pro nezávislé náhodné veličiny s c2 rozdělením se dá dokázat, že jejich součet má opět c2 rozdělení a počet stupňů volnosti je roven součtu stupňů volnosti jednotlivých veličin v součtu.

 Jak jsme již uvedli, c2 rozdělení má široké uplatnění především při statistických aplikacích. Uvedeme alespoň některé vlastnosti a možnosti použití.

  1. Pokud náhodné veličiny X1,X2,...,Xn mají normální rozdělení N(µ,s2) a jsou navzájem nezávislé, pak výběrový rozptyl

    vynásobený (n - 1) a vydělený s2 má rozdělení c2(n - 1).

    Tuto skutečnost můžeme stručně zapsat takto

      ~ c2 (n - 1)

    Tento fakt je zejména důležitý při statistickém testování hypotéz, o kterém uslyšíme v dalších kapitolách.

  2. c2 rozdělení se používá pro ověření nezávislosti náhodných veličin .

  3. Dále se používá k ověření na základě dat, zda dva či více výběrů jsou homogenní vzhledem k jisté veličině. Např. se posuzuje, zda politické názory obyvatel jsou různé v různých regionech apod.

  4. Pokud testujeme, zda náhodné veličiny pocházejí z určitého rozdělení, můžeme s úspěchem použít chí-kvadrát rozdělení. Tento test je znám pod názvem "test dobré shody".