F rozdělení

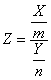
Posledním spojitým rozdělením, kterým se budeme zabývat, je F rozdělení. Toto rozdělení je odvozeno z podílu dvou nezávislých náhodných veličin (s chí-kvadrát rozdělením) dělených stupni volnosti. Tedy 

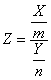
Nechť X a Y jsou nezávislé náhodné veličiny, přičemž X ~ c2(m) a Y ~ c2(n). Potom náhodná veličina

má Fisherovo-Snedecorovo rozdělení F(m,n) o m a n stupních volnosti.

Tento fakt budeme zapisovat Z ~ F(m,n). Z definice náhodné veličiny Z je zřejmé, že hustota je nenulová pouze pro z > 0. Její tvar je poměrně složitý a nebudeme jej proto uvádět. Kvantily tohoto rozdělení budeme opět značit dle zvyklostí a jejich hodnoty lze opět nalézt v tabulkách. Platí pro ně následující vztah:

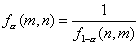
Z tohoto důvodu nebývají tabelovány všechny kvantily, ale pouze hodnoty pro a > 0.5 (resp. a < 0.5 - záleží na tabulkách). 

Pokud n > 2, existuje konečná střední hodnota a má tvar 

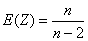
Střední hodnota náhodné veličiny Z s Fisherovým-Snedecorovým rozdělením - Z ~ F(m,n)

Pokud n > 4 existuje konečný rozptyl a je roven

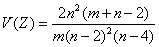
Rozptyl náhodné veličiny Z s Fisher-Snedecorovým rozdělením - Z ~ F(m,n)

Toto rozdělení má opět široké uplatnění, především při hodnocení výsledků statistických analýz. Používá se především: 

  1. K testu o shodnosti rozptylů dvou náhodných výběrů.

  2. K testům o shodě středních hodnot pro více náhodných výběrů.

  3. K testům v regresní analýze.