Dalším důležitým spojitým rozdělením, se kterým se budeme často setkávat, je Studentovo rozdělení nebo častěji označované jako t rozdělení. Název Studentovo rozdělení vznikl podle pána, který se nejmenoval Student, jak by se dalo očekávat. Tento pán se jmenoval William Sealy Gosset a nebyl povoláním statistikem, jak by se opět dalo očekávat. Byl povoláním chemik a začátkem našeho století pracoval v anglickém pivovaru Guinness. A toto rozdělení nevymyslel proto, že by se nudil, ale proto, že potřeboval vyvozovat na základě velmi malých vzorků použitelné závěry. A k těmto účelům se toto rozdělení používá dodnes. A to je konec pohádky. Ale ne, není to konec pohádky. Na jeho práci navázalo množství dalších statistiků; jmenujme alespoň R. A. Fishera, jehož jméno můžeme najít téměř ve všech směrech dalšího vývoje statistiky.
Po tomto malém odbočení se věnujme možnostem odvození tohoto rozdělení. Dá se poměrně snadno ukázat, že t rozdělení lze odvodit jako podíl dvou nezávislých náhodných veličin, z nichž jedna má normované normální rozdělení a druhá chí-kvadrát rozdělení. Protože však je to o trošičku složitější, formulujme toto odvození přesně.
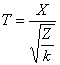
má Studentovo rozdělení s n stupni volnosti.
Tento fakt budeme značit T ~ t(n).
Hustota tohoto rozdělení má opět složitý tvar a nebudeme ji proto uvádět. Důležité je, že toto rozdělení je jednovrcholové a symetrické a tvar hustoty je velmi podobný hustotě normálního rozdělení (je definováno pro t od -Ą do +Ą). Liší se od něj v podstatě jen tím, že t rozdělení má "těžší" konce. Hustotu Studentova rozdělení si pro různé stupně volnosti můžete nechat nakreslit na stránce http://www-stat.stanford.edu/~naras/jsm/TDensity/TDensity.html.
E(X) = 0 pro n > 1
D(X) = n/(n - 2) pro n > 2
Kvantily budeme opět značit obvyklým způsobem. Jejich hodnoty lze nalézt v tabulkách. Z důvodu symetrie jsou tam uvedeny pouze od 50%-ního kvantilu výše, neboť mezi nimi platí vztah
tp = - t1-p.
t rozdělení má široké uplatnění. Uvedeme alespoň některé možnosti použití.
Užívá se k testování hypotéz o střední hodnotě náhodného výběru, pokud je rozptyl neznámý. Mělo by platit, že tento náhodný výběr pochází z normálního rozdělení, ale tento předpoklad je většinou alespoň přibližně splněn, jak dále poznáme.
Užívá se k testování hypotéz o shodě středních hodnot dvou náhodných výběrů, se stejnými předpoklady jako v 1. - navíc musí být tyto výběry nezávislé. Jako příklad můžeme uvést např. test pro porovnání výnosnosti dvou různých druhů pšenice, porovnání účinnosti dvou diet apod.
t rozdělení je vhodným prostředkem pro analýzu výsledků regresní analýzy.